Petites notions mathématiques concernant la forêt
La surface forestière
Il faut distinguer :
La surface à plat ou surface horizontale, celle indiquée par le cadastre, utilisée par les impôts et reportée dans les titres de propriété,
Par opposition à la surface du sol, réelle ou surface gauche,
La différence provient de plusieurs facteurs :
- La pente du terrain
- La courbure de la terre : il faut s’en préoccuper pour les grandes surfaces ;
- L’altitude également : l’écartement des distances est plus grand dans les hauteurs
Le calcul traditionnel à la chaine d’arpenteur et celui fait à partir du positionnement GPS peuvent réserver des surprises !
La surface en pente ou en suivant la pente.
En topographie toutes les distances sont
données en distances horizontales.
La distance mesurée sur le terrain (suivant la pente) est projetée à
l'horizontale à l'aide de l'angle vertical mesuré lors des opérations de terrain.
On projette aussi les distances terrains "au niveau zéro" en fonction
de l'altitude au centre de la distance mesurée.
La distance est aussi corrigée de la déformation due au système de projection
("correction Lambert")
L'écart entre la distance mesurée sur le terrain entre 2 points et la distance
calculée par les coordonnées de ces 2 points (celle indiquée sur un plan) est fonction :
1) de la pente, 2) de l'altitude, 3) de la distance par rapport à l'axe de la
projection cartographique (si grande distance entre les 2 points)
Et donc une distance de 100 m donnée par un plan cadastral correspond, si elle est prise perpendiculairement à une pente de 45°, à une distance de 141,42 m en suivant la topographie du terrain.
Un calcul des mesures réelles est nécessaire pour les terrains en pente, en cas de plantation – nombre de plants à prévoir – ou en cas de clôture – quelle longueur prévoir -
La méthode pour figure simple, le triangle : la formule est la suivante : appelons « L » la longueur sur un plan et « l » largeur, « a » l'angle moyen trouvé en radians dans le sens de la longueur et « b » celui de la largeur, enfin « LR » et « lr » les "vraies " dimensions :
SURFACE REELLE = LR x lr =L/COSa x l/cos b
A comparer avec la surface à plat sur plan = « L » x « l »
La méthode pour figure quelconque ou complexe : pour
des formes irrégulières il faut pratiquer par décomposition géométriques, et
donc diviser en surfaces connues.
Le plus simple est de décomposer l'ensemble en triangle. On mesure les longueurs
des segments ainsi tracés et on calcul la surface de chaque triangle.
Pour calculer une surface gauche, calculer la longueur de chaque segment en
considérant cette fois ci une figure géométrique positionnée verticalement.
Puis calculer la surface de chaque surface projetée. Par exemple pour une pente
à 40°, la longueur du segment suivant la pente (donc l'hypoténuse du triangle)
est égale à longueur du segment horizontal divisé par cos 40°.
Pour un résultat global le plus proche de la réalité possible, calculer l'aire de
chaque figure géométrique par deux méthodes différentes. Par exemple dans un
triangle il y a 3 bases et 3 hauteurs. Donc 3 possibilités de calculer sa
surface. La bonne surface du terrain sera la moyenne des aires globales
calculées.
Un exemple de calcul :
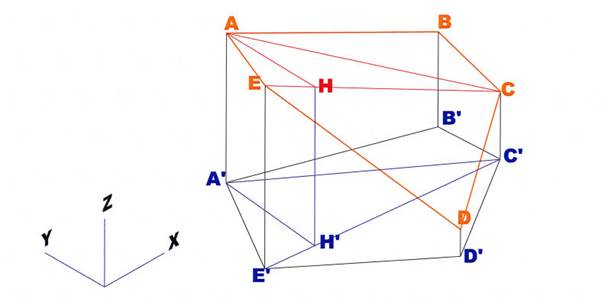
Soit la surface gauche A B C D E
Sa projection orthogonale A' B' C' D' E'
On décompose cette surface en figures géométriques simples.
Soit 3 triangles: A' B' C'; A'C' E' et C' D' E'
Considérons le triangle A'C'E' et sa hauteur A'H'
Les valeurs de C' E' et de A' H' sont mesurées sur plan.
La précision de lecture et de l'ordre du cm sur un plan au 1/200 et du
décimètre sur un plan au 1/2000.
Cherchons la longueur du segment CE
![]() h=EE' - CC'
h=EE' - CC'
CE² = ![]() h² + C'E'²
h² + C'E'²
Cherchons la longueur du segment AH
![]() h=AA' - HH'
h=AA' - HH'
AH² = ![]() h² + A'H'²
h² + A'H'²
La surface du triangle ACE devient: CE x AH / 2
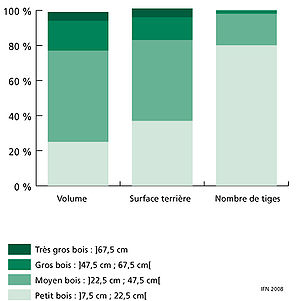
La surface terrière (Source Wikipédia)
La surface terrière correspond, pour un arbre donné, en France, à la surface de la section d'un arbre mesurée à 1,30 mètre du sol (environ 4,5 pieds de hauteur dans le système anglo-saxon, et autrefois « à hauteur d'épaule »). Selon les pays et époques, cette mesure peut être faite ou avoir été faite à une hauteur comprise entre 1 et 1,5 m au-dessus du niveau du sol. C'est une mesure souvent plus approximative en zone tropicale pour les grands arbres, car pour certaines espèces, leurs « contreforts » peuvent empêcher de faire une mesure pertinente à cette hauteur.
La surface terrière totale ou moyenne d'une aire donnée (arbres dispersés, alignés ou peuplement forestier, agrosylviculture, bocage, verger, parc urbain, etc.) peut être calculée par la somme des surfaces terrières de tous les arbres de cette aire ; elle s'exprime habituellement en m²/ha. Le nombre calculé pour un ha permet une extrapolation approximative pour une surface homogène plus grande. Ainsi une surface terrière moyenne peut être calculée pour un pays. Par exemple, en France métropolitaine, la surface terrière moyenne est estimée à 21,7 m2/ha par l'Inventaire forestier national pour la forêt publique de métropole. À l'échelle d'un pays, ce chiffre ne devrait pas théoriquement beaucoup évoluer dans le temps, sauf à la suite d'incendies majeurs, épidémies majeures ou tempêtes importantes, qui peuvent aussi être des indices des premiers impacts globaux de modifications climatiques. Ainsi en France, les 19 690 000 m3 de chablis résultants des deux tempêtes de décembre 1999 représentaient selon l'ONF plus de 7 % de la ressource totale en bois des forêts domaniales.
Remarques :
- La surface terrière d'un arbre est d'autant plus élevée que l'arbre est gros.
- La surface terrière d'un peuplement est d'autant plus élevée que le peuplement est dense.
- Pour des raisons de temps et parce qu'une grande partie des jeunes arbres seront éliminés les premières années lors de la compétition pour la lumière, on ne mesure généralement la surface terrière que pour les tiges de plus de 10 cm de diamètre (7,5 cm dans le protocole de l'Inventaire forestier national).
Utilisation
La surface terrière est l’un des indicateurs utilisé pour la gestion sylvicole ou lors de l'étude de peuplements forestiers. Le suivi dans le temps de cette mesure donne en effet un indice précis de la productivité ligneuse d'une parcelle, via la vitesse de croissance (en diamètre) des arbres. La surface terrière est aussi un indice d'occupation du sol et de l'espace par les arbres. Pour être plus réaliste cet indice doit être croisé avec la hauteur des arbres, notamment pour les espèces qui croissent peu en largeur et rapidement en hauteur, tout particulièrement en forêt dense.
La distance des arbres de plantation – la densité -
Plantation en carré : facilite pour l’entretien le passage des engins
|
Tableau du Nombre d'arbres par hectare selon différentes distances de plantation * |
||||||||||||||||||
|
Distance entre les arbres (m°) |
Distance entre les rangs (m’) |
|||||||||||||||||
|
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
9,5 |
10 |
||
|
1,5 |
3333 |
2667 |
2222 |
1905 |
1667 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2500 |
2000 |
1667 |
1428 |
1250 |
1111 |
1000 |
909 |
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
1600 |
1333 |
1143 |
1000 |
889 |
800 |
727 |
667 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1111 |
952 |
833 |
741 |
667 |
606 |
555 |
513 |
|
|
|
|
|
|
|
|
|
3,5 |
|
|
|
816 |
714 |
635 |
571 |
519 |
476 |
440 |
408 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
625 |
555 |
500 |
455 |
417 |
385 |
357 |
333 |
|
|
|
|
|
|
|
4,5 |
|
|
|
|
|
494 |
444 |
404 |
370 |
342 |
317 |
296 |
278 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
400 |
364 |
333 |
308 |
286 |
267 |
250 |
235 |
|
|
|
|
|
5,5 |
|
|
|
|
|
|
|
330 |
303 |
279 |
260 |
242 |
227 |
214 |
202 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
278 |
256 |
238 |
222 |
208 |
196 |
185 |
175 |
|
|
|
6,5 |
|
|
|
|
|
|
|
|
|
236 |
220 |
205 |
192 |
181 |
171 |
162 |
154 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
204 |
190 |
178 |
168 |
159 |
150 |
143 |
|
* Pour trouver le nombre d'arbres par hectare en fonction d'une autre distance de plantation, multiplier la distance entre les arbres (m°) par la distance entre les rangs (m’) et diviser 10 000 par le chiffre obtenu.
Plantation en quinconce : meilleure occupation spatiale ; à privilégier pour les petites parcelles, les bouquets d’arbres, les terrains en pente, les brise-vents …
Une plantation de 1200 tiges à l’hectare donne un écartement d’arbres de 2,9 m pour les plantations en carré, de 3,1 m pour les plantations en quinconce
Pour les terrains en pente, l’écartement est plus grand, soit de pied à pied soit de cime à cime ; en reprenant l’exemple précédent de 45° de pente, nous trouvons 4,10 m pour les plantations en carré, 4,38 m pour celles en quinconce.
Avec un écartement de 2,9 m, il faut envisager deux éclaircies successives avant une coupe définitive, alors qu’avec un écartement de 4,38 m il suffirait d’une seule éclaircie avant la coupe.
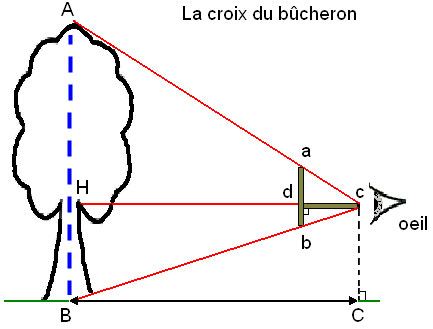
La hauteur des arbres
Prendre 2 baguettes de même dimension et droite (ab =
cd)
Placer la 1ère baguette en position horizontale (parallèle au plan du sol) et
la 2ème perpendiculaire à la 1ère
Se placer face à l’arbre, à une distance approximativement voisine de sa
hauteur.
Avancer ou reculer tout en faisant coulisser la baguette verticale de manière à
faire coïncider :
· Le pied de l’arbre, le bas de la baguette verticale et son œil sur une même ligne (cB),
· La cime de l’arbre, le haut de la baguette verticale et son œil sur une même ligne (cA)
Lorsque les 2 extrémités de l’arbre correspondent aux extrémités de la
baguette verticale, mesurer la distance vous séparant de l’arbre (BC)
La hauteur de l’arbre (AB) est alors égale à la distance BC
Le cubage des arbres
Pour calculer le volume approximatif d'un tronc d'arbre (le
cubage), on utilise la formule suivante :
![]()
où « V » est le volume recherché, « C » est le périmètre de la section moyenne, c'est à dire la section pratiquée à égale distance des extrémités et « l » est la longueur du tronc
Exemple : calculer « C », puis le cubage « V » d'un arbre dont le diamètre de la section moyenne est 52 cm et la longueur 3 m (52 cm étant = à 0,52 m)
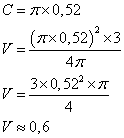
Le volume est donc de 0,6 m3 environ.
Quelques chiffres
Quelques chiffres sont seulement à aligner en ce qui concerne :
Les limites forestières :
- Distance de plantation sur une propriété riveraine
- Distance de plantation sur la voie publique
- Distance sur un cours d’eau
L’évaluation d’une forêt :
- Méthode comparative
- Méthode analytique, comprenant les valeurs et facteurs suivants :
- Valeur du foncier, le sol
- Valeur des pieds de bois
- Le facteur chasse
- Le facteur environnement, paysagé
- Le facteur d’accessibilité forestière (pour le débardage)